At Venerable Bede CE Academy, we strive towards shaping confident, happy and resilient mathematicians who relish a challenge. We intend for all pupils to become independent, reflective thinkers, whose skills not only help them in Maths but also support them across the curriculum. Mathematics is essential to all aspects of life and, with this in mind; we aim to ensure that our pupils develop a positive and enthusiastic attitude that will stay with them throughout their life. Our DEEP curriculum intends to equip pupils with a dynamic set of tools to help them understand and change the world. These tools include making connections, logical reasoning, and the ability to think in abstract ways. Our ultimate aim is for our pupils to achieve to the best of their ability. For our pupils to be confident mathematicians in our subject, across the wider curriculum and also in their day-to-day lives.
DEEP Curriculum Overview
Through our DEEP Mathematics curriculum, all pupils will learn:
- To become fluent in the fundamentals of Mathematics through varied and frequent practice of increasingly complex problems over time.
- To develop an ability to think and reason mathematically;
- To solve problems by applying Mathematics to a variety of routine and non-routine problems with increasing sophistication, including breaking down problems into a series of simpler steps and persevering in seeking solutions.
- To realise the application of Mathematics in the world around us;
- To develop a firm foundation for appropriate further study.
- To engage with, explore, enjoy and succeed in Mathematics.
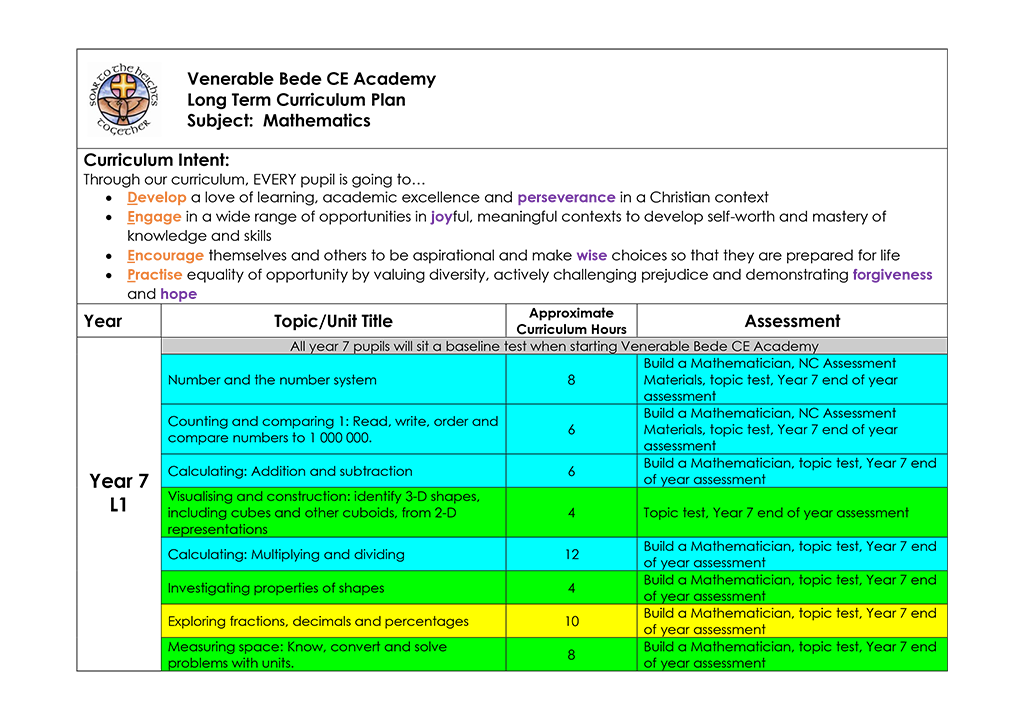
Topics / Areas of Study
Click image to read in full.